The quest for new, innovative derivative products pushes financial institutions to design and develop more exotic forms of structured products, many of which are aimed toward the specific needs of the customers. Recently, there has been a growing popularity for path dependent options, so named since their payoff structures are related to the underlying asset price path history during the whole or part of the life of the option. The barrier option is the most popular path dependent option that is either nullified, activated or exercised when the underlying asset price breaches a barrier during the life of the option.
Barrier options
Options with the barrier feature are considered to be the simplest types of path de- pendent options. Barrier option’s distinctive feature is that the payoff depends not only on the final price of the underlying asset, but also on whether the asset price has breached (one-touch) some barrier level during the life of the option. An out-barrier option (or knock-out option) is one where the option is nullified prior to expiration if the underlying asset price touches the barrier. The holder of the option may be compensated by a rebate payment for the cancellation of the option. An in-barrier option (or knock-in option) is one where the option only comes in existence if the asset price crosses the in-barrier, though the holder has already paid the option premium up front. When the barrier is upstream with respect to the asset price, the barrier option is called an up-option; otherwise, it is called a down-option. One can identify eight types of European barrier options, such as down-and-out calls, up-and-out calls, down-and-in puts, down-and-out puts, etc.
Consider a portfolio of one European in-option and one European out-option: both have the same barrier, strike price and date of expiration. The sum of their values is simply the same as that of a corresponding European option with the same strike price and date of expiration. Provided there are no rebated payments we have the following in-out parity
\[C_{vanilla} = C_{down-and-in} + C_{down-and-out},\] \[P_{vanilla} = P_{down-and-in} + P_{down-and-out},\]where c and p denote call and put values, respectively. Therefore, the value of an out- option can be found easily once the value of the corresponding in-option is available, or vice versa.
Fortunately for European barrier options, closed form solutions exist under the Black-Scholes framework. We present below the formula for the down-and-in call option for \(H \geq X\).
\[C_{do} = S_0N(x_1)e^{-q\tau} - Xe^{-r\tau}N(x_1-\sigma\sqrt{\tau}) - S_0e^{-q\tau}(H/S_0)^{2\lambda}N(y_1) + Xe^{-r\tau}(H/S_0)^{2\lambda-2}N(y_1-\sigma\sqrt{t}),\] \[C_{di} = C - C_{do},\]with
- \(C\): the value of the vanilla call (with no barrier),
- \(C_{do}\): the value of the down-and-out call,
- \(C_{di}\): the value of the down-and-in call,
- \(q\): the continuous dividend rate,
- \(H\): the barrier level,
- \(S_0\): current underlier price,
- \(X\): strike price,
- \(\tau\): time to maturity, in years,
- \(r\): risk free rate,
- \(\lambda = \frac{r-q+\sigma^2/2}{\sigma^2}\),
- \[x_1 = \frac{\ln(S_0/H)}{\sigma\sqrt{\tau}} + \lambda \sigma \sqrt{\tau},\]
- \[y_1 = \frac{\ln(H/S_0)}{\sigma\sqrt{\tau}} + \lambda \sigma \sqrt{\tau}\]
% Black Scholes program for European down and in call
% call syntax: c = BS_EurDownInCall(S0,X,r,T,H,sigma,q)
function value = BS_EurDownInCall( S0,X,r,T,H,sigma,q)
lambda = (r - q + sigma^2/2)/(sigma^2);
x1 = log(S0/H)/(sigma*sqrt(T)) + lambda*sigma*sqrt(T);
y1 = log(H./S0)/(sigma*sqrt(T)) + lambda*sigma*sqrt(T);
C1 = S0.*normcdf(x1)*exp(-q*T);
C2 = X*exp(-r*T)*normcdf(x1 - sigma*sqrt(T));
C3 = S0.*exp(-q*T).*(H./S0).^(2*lambda).*normcdf(y1);
C4 = X*exp(-r*T)*(H./S0).^(2*lambda - 2).*normcdf(y1 - sigma*sqrt(T));
value = BS_EurVanillaCall(S0,X,r,T,sigma,q) - C1 + C2 + C3 - C4;
endBarrier vs. Vanilla : which is cheaper?
We conjecture that barrier options would have a lower price because they carry the risk of being nullified and hence expire worthless. To verify this, we will fix a barrier level (H=1.3) and a strike price (X=1.1), then calculate the price of each type of options for different values of \(S_0\).
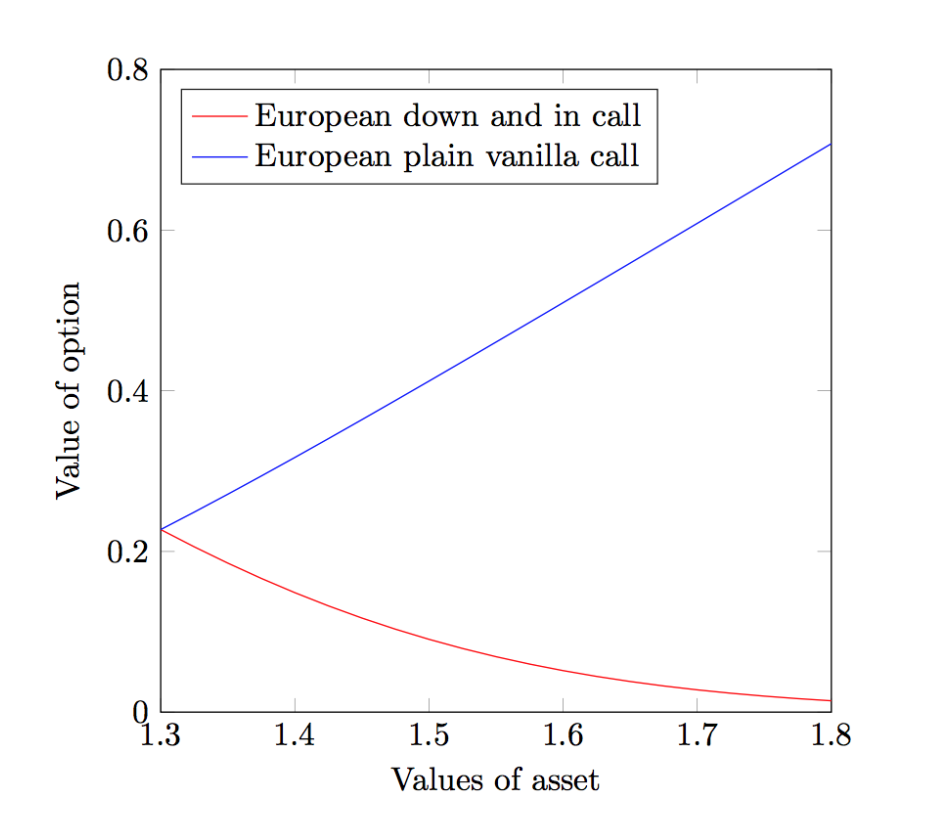
Indeed the barrier option is cheaper than its vanilla counterpart! The only time when the two options have the same value is when \(S_0 = H = 1.3\). As \(S_0\) increases, the distance between \(H\) and \(S_0\) grows larger, the down-and-in call becomes increasingly cheaper than the vanilla call. It is because as \(S_0\) moves further away from \(H\), the lower the probability that \(S_0\) can approach the barrier and become activated.
Reference
- Yue-Kuen Kwok. Mathematical Models of Financial Derivatives. Springer, Second edition.